Giới hạn của hàm số sau đây khi x tiến đến 2: f( x ) = dx^2 - 3x + 2( x - 2 )^2 bằng bao nhiêu:

Câu hỏi
Nhận biếtGiới hạn của hàm số sau đây khi x tiến đến 2: \(f\left( x \right) = \dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}}\) bằng bao nhiêu:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Nhập hàm số \(\dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}}\) :
Nhấn phím [CALC], chọn \(x = 2 + 0,000001\) ta được kết quả 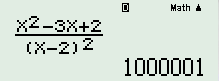 \( \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}} = + \infty \)
Nhấn phím [CALC], chọn \(x = 2 - 0,000001\) ta được kết quả 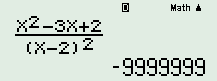 \( \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}} = - \infty \)
\( \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 3x + 2}}{{{{\left( {x - 2} \right)}^2}}} = - \infty \)
Chọn A.









