Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho SI SO = 2 3 B

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho \({{SI} \over {SO}} = {2 \over 3}\), BI cắt SD tại M và DI cắt SB tại N. MNBD là hình gì?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
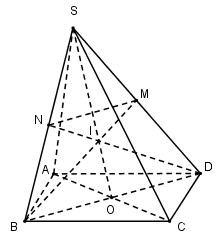
Dễ thấy I là trọng tâm của tam giác SBD nên BI, DI là các đường trung tuyến của tam giác SBD.
Suy ra M, N lần lượt là trung điểm của SD và SB.
Nên MN là đường trung bình của tam giác BCD \( \Rightarrow \) MN // BD.
Vậy tứ giác MNBD là hình thang.
Chọn A.









