Cho tứ diện ABCD có I và J lần lượt là trọng tâm của tam giác ABC và ABD. Đường thẳng IJ song song v

Câu hỏi
Nhận biếtCho tứ diện ABCD có I và J lần lượt là trọng tâm của tam giác ABC và ABD. Đường thẳng IJ song song với đường thẳng:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
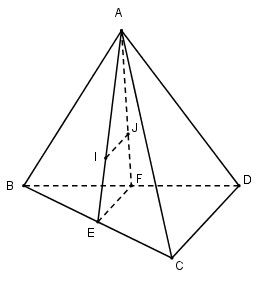
Gọi E, F lần lượt là trung điểm của BC và BD ta có:
\(\eqalign{ & I \in AE\,;\,{{AI} \over {AE}} = {2 \over 3} \cr & J \in AF\,;\,{{AJ} \over {AF}} = {2 \over 3} \cr} \)
Xét trong mp(AEF) ta suy ra IJ // EF (Định lí Ta – let đảo)
Mà EF là đường trung bình của tam giác BCD nên EF // CD
Vậy IJ // CD.
Chọn D.









