[LỜI GIẢI] Cho tứ diện ABCD . Gọi I ; J lần lượt là trung điểm các cạnh AB ; CD . - Tự Học 365
LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY
XEM CHI TIẾT

Cho tứ diện ABCD . Gọi I ; J lần lượt là trung điểm các cạnh AB ; CD .

Câu hỏi

Nhận biết

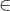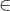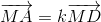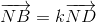Cho tứ diện ABCD . Gọi I ; J lần lượt là trung điểm các cạnh AB ; CD . Lấy điểm M in AD ; N in BC sao cho overrightarrow {MA} = koverrightarrow {MD} và overrightarrow {NB} = koverrightarrow {ND} ( k ≠ 1) . Chứng minh 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.


Đáp án đúng:

Lời giải của Tự Học 365

Giải chi tiết:

Ta có :

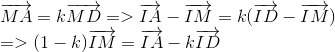
egin{array}{l} overrightarrow {MA} = koverrightarrow {MD} = > overrightarrow {IA} - overrightarrow {IM} = k(overrightarrow {ID} - overrightarrow {IM} )\ = > (1 - k)overrightarrow {IM} = overrightarrow {IA} - koverrightarrow {ID} end{array}

Chứng minh tương tự ta có : 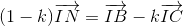(1 - k)overrightarrow {IN} = overrightarrow {IB} - koverrightarrow {IC}

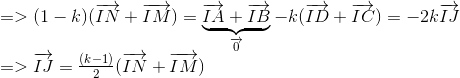
egin{array}{l} = > (1 - k)(overrightarrow {IN} + overrightarrow {IM} ) = underbrace {overrightarrow {IA} + overrightarrow {IB} }_{overrightarrow 0 } - k(overrightarrow {ID} + overrightarrow {IC} ) = - 2koverrightarrow {IJ} \ = > overrightarrow {IJ} = frace_(k - 1){2}(overrightarrow {IN} + overrightarrow {IM} ) end{array}

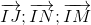Suy ra overrightarrow {IJ} ;overrightarrow {IN} ;overrightarrow {IM} đồng phẳng 

Vậy 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan