Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E, F, G

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy ABCD là hình bình hành tâm O. Gọi E, F, G lần lượt là trung điểm của SA, BC, SD.
a) Xác định giao tuyến d của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
b) Chứng minh rằng EF // (GAO).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
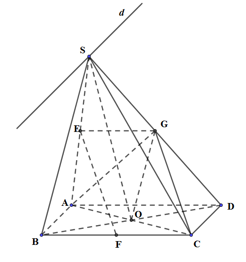
a) Ta có: \(\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\CD \subset \left( {SCD} \right)\\AB//CD\\\left( {SAB} \right) \cap \left( {SCD} \right) = d\end{array} \right. \Rightarrow d//AB//CD\)
Mặt khác \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) \Rightarrow \) Giao tuyến d của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng qua S và song song với AB.
b) O là tâm của hình bình hành ABCD \( \Rightarrow O\), A, C thẳng hàng \( \Rightarrow C \in \left( {GAO} \right)\)
Ta có: EG là đường trung bình của tam giác SAD \( \Rightarrow EG = \frac{1}{2}AD\)
Mà \(FC = \frac{1}{2}BC;\,\,AD = BC \Rightarrow EG = FC \Rightarrow EGCF\) là hình bình hành \( \Rightarrow EF//CG\)
\( \Rightarrow EF//\left( {GAC} \right)\) hay \( \Rightarrow EF//\left( {GAO} \right)\) (đpcm).









