Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD,AB = 2CD). Gọi

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang (\(AB//CD,\,\,AB = 2CD\)). Gọi \(M\) là trung điểm của cạnh \(SC\).
a) Xác định giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
b) Xác định giao điểm \(K\) của đường thẳng \(AM\) với \(mp\left( {SBD} \right)\). Tính tỉ số \(\dfrac{{AK}}{{AM}}\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Xác định giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
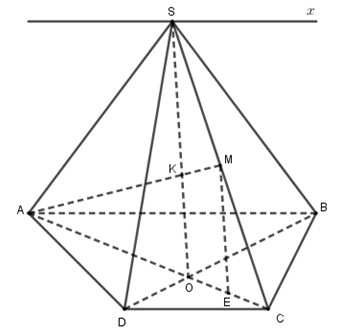
\(S\) là điểm chung của \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
\(AB//CD;\,\,AB \subset \left( {SAB} \right);\,\,CD \subset \left( {SCD} \right)\).
Suy ra \(\left( {SAB} \right) \cap \left( {SCD} \right) = Sx//AB//CD\).
b) Xác định giao điểm \(K\) của đường thẳng \(AM\) với \(mp\left( {SBD} \right)\). Tính tỉ số \(\dfrac{{AK}}{{AM}}\).
Ta có: \(AM \subset \left( {SAC} \right)\).
Dễ thấy \(S \in \left( {SAC} \right) \cap \left( {SBD} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Khi đó \(O \in AC \subset \left( {SAC} \right),O \in BD \subset \left( {SBD} \right)\) nên \(O \in \left( {SAC} \right) \cap \left( {SBD} \right)\).
Do đó \(SO = \left( {SAC} \right) \cap \left( {SBD} \right)\).
Trong \(\left( {SAC} \right)\), gọi \(K = AM \cap SO\) thì \(K \in AM,K \in SO \subset \left( {SBD} \right)\) nên \(K = AM \cap \left( {SBD} \right)\).
Do \(AB//CD\) nên \(\dfrac{{OC}}{{OA}} = \dfrac{{CD}}{{AB}} = \dfrac{1}{2}\)\( \Rightarrow OA = \dfrac{2}{3}AC,OC = \dfrac{1}{3}AC\).
Gọi \(E\) là trung điểm của \(OC\) suy ra \(ME\) là đường trung bình của \(\Delta SCO\)
\( \Rightarrow ME//SO\).
Mà \(OE = \dfrac{1}{2}OC = \dfrac{1}{2}.\dfrac{1}{3}AC = \dfrac{1}{6}AC\) \( \Rightarrow AE = AO + OE\) \( = \dfrac{2}{3}AC + \dfrac{1}{6}AC = \dfrac{5}{6}AC\)
\( \Rightarrow \) \(\dfrac{{AK}}{{AM}} = \dfrac{{AO}}{{AE}} = \dfrac{4}{5}\).









