Cho hình hộp ABCD.A’B’C’D’. M, N, P là trung điểm của B’C’, AB, DD’. C

Câu hỏi
Nhận biếtCho hình hộp ABCD.A’B’C’D’. M, N, P là trung điểm của B’C’, AB, DD’. Chứng minh \(\left( MNP \right)\parallel \left( AB'D' \right)\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
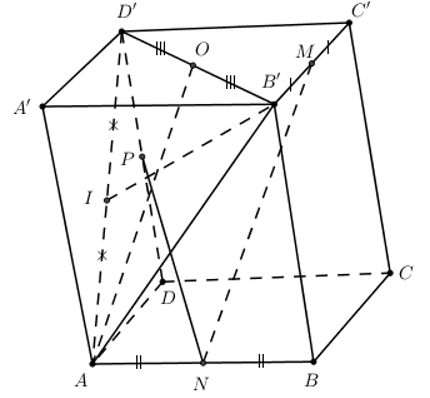
+) Vẽ O là trung điểm của B’D’.
+) Tam giác B’C’D’ có OM là đường trung bình \(\Rightarrow \left\{ \begin{align} & OM\parallel C'D' \\ & OM=\frac{1}{2}C'D' \\\end{align} \right.\,\left( 1 \right)\)
+)
\(\left\{ \begin{array}{l}
C'D'\parallel AB\\
C'D' = AB
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
AN\parallel C'D'\\
AN = \frac{1}{2}C'D'
\end{array} \right.\,\,\left( 2 \right)\)
Từ (1) và (2) \(\Rightarrow \left\{ \begin{align} & OM\parallel AN \\ & OM=AN \\\end{align} \right.\Rightarrow \) Tứ giác MNAO là hình bình hành \(\Rightarrow MN\parallel AO\,\,\left( 3 \right)\)
+) Vẽ I là trung điểm của AD’. Chứng minh tương tự ta có \(MP\parallel B'I\,\left( 4 \right)\)
+) Từ (3), (4) \(\Rightarrow \left( MNP \right)\parallel \left( AB'D' \right)\)









