Cho hình lập phương ABCD.A'B'C'D' cạnh a. Trên các cạnh DC và BB' lấy

Câu hỏi
Nhận biếtCho hình lập phương \(ABCD.A'B'C'D' \) cạnh \(a \). Trên các cạnh \(DC \) và \(BB' \) lấy các điểm \(M \) và \(N \) sao cho \(MD = NB = x \, \, \, \left( {0 \le x \le a} \right) \). Khẳng định nào sau đây là đúng?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
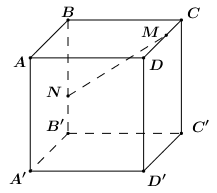
Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\,\,\overrightarrow {AB} = \overrightarrow b ,\,\,\overrightarrow {AD} = \overrightarrow c \).
Ta có:
\(\begin{array}{l}\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \left( {\overrightarrow {AB} + \overrightarrow {BN} } \right) - \left( {\overrightarrow {AD} + \overrightarrow {DM} } \right)\\ = \left( {\overrightarrow b + \dfrac{x}{a}.\overrightarrow a } \right) - \left( {\overrightarrow c + \dfrac{x}{a}\overrightarrow b } \right) = \dfrac{x}{a}\overrightarrow a + \left( {1 - \dfrac{x}{a}} \right)\overrightarrow b - \overrightarrow c \end{array}\)
Từ đó ta có:
\(\begin{array}{l}\overrightarrow {AC'} .\overrightarrow {MN} = \left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\left[ {\dfrac{x}{a}\overrightarrow a + \left( {1 - \dfrac{x}{a}} \right)\overrightarrow b - \overrightarrow c } \right]\\ = \dfrac{x}{a}{\overrightarrow a ^2} + \left( {1 - \dfrac{x}{a}} \right){\overrightarrow b ^2} - {\overrightarrow c ^2}\,\,\,\left( {Do\,\,\overrightarrow a \overrightarrow b = 0;\,\,\overrightarrow a \overrightarrow c = 0;\,\,\overrightarrow b \overrightarrow c = 0} \right)\\ = \dfrac{x}{a}.{a^2} + \left( {1 - \dfrac{x}{a}} \right).{a^2} - {a^2}\\ = x.a + {a^2} - x.a - {a^2}\\ = 0\end{array}\)
Vậy \(AC' \bot MN\).
Chọn A.









