Cho hình chóp S.ABCD có đáy là hình bình hành. Mặt phẳng ( alpha ) cắ

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy là hình bình hành. Mặt phẳng \( \left( \alpha \right) \) cắt SA, SB, SC, SD theo thứ tự lần lượt tại A’, B’, C’, D’ (không đồng thời trùng với các đầu mút). \(A'B'C'D' \) là hình bình hành khi và chỉ khi:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
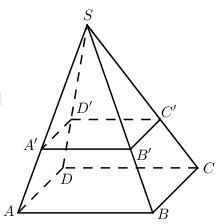
Do A’, B’, C’, D’ không đồng thời trùng với các đầu mút nên loại đáp án C.
Gọi a là đường thẳng qua S và song song với AB, b là đường thẳng qua S và song song với AD.
A’B’C’D’ là hình bình hành khi và chỉ khi \(\left\{ \begin{array}{l}A'B'//C'D'\\A'B' = C'D'\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}a = \left( {ABC} \right) \cap \left( {SCD} \right)\\A'B'//C'D'\\A'B' \subset \left( {ABC} \right),\,\,C'D' \subset \left( {SCD} \right)\end{array} \right. \Rightarrow A'B'//a\)
Suy ra A’B’ // AB (1)
Tương tự ta có: \(\left\{ \begin{array}{l}b = \left( {ABD} \right) \cap \left( {SBC} \right)\\A'D'//B'C'\\A'D' \subset \left( {ABD} \right),\,\,C'B' \subset \left( {SBC} \right)\end{array} \right. \Rightarrow A'D'//b\)
Suy ra A’D’ // AD (2).
Từ (1) và (2) \( \Rightarrow \left( {A'B'C'D'} \right)//\left( {ABCD} \right)\) hay \(\left( \alpha \right)//\left( {ABCD} \right)\).
Chọn A.









