Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I J lần lượt là trung điểm

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
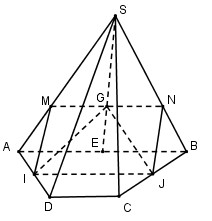
Ta có: ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD.
\( \Rightarrow \) IJ // AB // CD.
\(\left\{ \matrix{ G \in \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) \hfill \cr AB \subset \left( {SAB} \right) \hfill \cr {\rm{IJ}} \subset \left( {{\rm{IJ}}G} \right) \hfill \cr AB//{\rm{IJ}} \hfill \cr} \right. \Rightarrow \) Trong (SAB) qua G kẻ MN // AB \(\left( {M \in SA;N \in SB} \right)\)
\( \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN.\) và MN // IJ // AB // CD.
Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI.
G là trọng tâm của tam giác SAB và MN // AB nên theo định lí Ta-let ta có:
\({{MN} \over {AB}} = {{SG} \over {SE}} = {2 \over 3}\) (Với E là trung điểm của AB).
\( \Rightarrow MN = {2 \over 3}AB\)
Lại có: IJ là đường trung bình của hình thang ABCD nên \({\rm{IJ}} = {{AB + CD} \over 2}.\)
Để hình thang MNJI trở thành hình bình hành thì cần điều kiện MN = IJ.
\( \Rightarrow {2 \over 3}AB = {1 \over 2}\left( {AB + CD} \right) \Leftrightarrow {1 \over 6}AB = {1 \over 2}CD \Leftrightarrow AB = 3CD.\)
Chọn D.









