Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 6 cm. Tính khoảng cách từ điểm B đến mặt ph

Câu hỏi
Nhận biếtCho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng 6 cm. Tính khoảng cách từ điểm B đến mặt phẳng \((SCD)\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
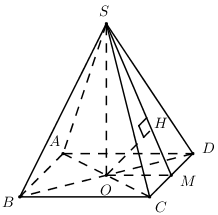
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
Gọi \(M\) là trung điểm của \(CD\) ta có \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right)\).
Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có
\(\left\{ \begin{array}{l}OH \bot SM\\OH \bot CD\end{array} \right. \Rightarrow OH \bot \left( {SCD} \right) \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OH\).
Ta có \(BO \cap \left( {SCD} \right) = D \Rightarrow \frac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \frac{{BD}}{{OD}} = 2\).
\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right) = 2OH\).
Ta có \(OM\) là đường trung bình của \(\Delta ACD \Rightarrow OM = \frac{1}{2}AD = 3\,\,\left( {cm} \right)\).
Trong \(\Delta SOC\) có: \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{6^2} - {{\left( {\frac{{6\sqrt 2 }}{2}} \right)}^2}} = 3\sqrt 2 \) (cm).
Áp dụng hệ thức lượng trong tam giác vuông \(SOM\) ta có:
\(OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \frac{{3\sqrt 2 .3}}{{\sqrt {18 + 9} }} = \sqrt 6 \).
Vậy \(d\left( {B;\left( {SCD} \right)} \right) = 2\sqrt 6 \,\,\left( {cm} \right)\).
Chọn C.









