Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây là sai?
Câu hỏi
Nhận biếtCho tứ diện \(ABCD\) có \(AC = AD\) và \(BC = BD\). Gọi \(I\) là trung điểm của \(CD\). Khẳng định nào sau đây là sai?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
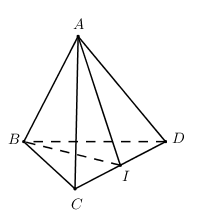
\(\Delta ACD\) và \(\Delta BCD\) cân tại \(A,\,\,B \Rightarrow AI \bot CD,\,\,BI \bot CD \Rightarrow CD \bot \left( {ABI} \right)\).
\( \Rightarrow \left\{ \begin{array}{l}\left( {ACD} \right) \bot \left( {AIB} \right)\\\left( {BCD} \right) \bot \left( {AIB} \right)\end{array} \right. \Rightarrow \) Đáp án A, B đúng.
Ta có
\(\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\\left( {ACD} \right) \supset AI \bot CD\\\left( {BCD} \right) \supset BI \bot CD\end{array} \right. \Rightarrow \angle \left( {\left( {ACD} \right);\left( {BCD} \right)} \right) = \angle \left( {AI;BI} \right) = \angle AIB\)
\( \Rightarrow \) Đáp án C đúng.
Chọn D.
