Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Góc giữa hai đường thẳng CD' và A'C' bằng

Câu hỏi
Nhận biếtCho hình lập phương ABCD.A’B’C’D’ có cạnh bằng \(a\). Góc giữa hai đường thẳng \(CD'\) và \(A'C'\) bằng
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
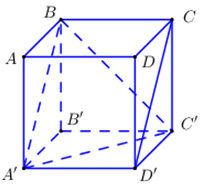
Ta có: \(CD'//A'B \Rightarrow \angle \left( {CD';A'C'} \right) = \angle \left( {A'B;A'C'} \right)\).
Áp dụng định lí Pytago ta tính được \(A'B = A'C' = BC' = a\sqrt 2 \Rightarrow \Delta A'BC'\) đều
\( \Rightarrow \angle \left( {A'B;A'C'} \right) = \angle BA'C' = {60^0}\).
Vậy \(\angle \left( {CD';A'C'} \right) = {60^0}\).
Chọn C.









