Gọi ( alpha ) là mặt phẳng qua O và song song với mặt phẳng (BEF). Gọi P là giao điểm của SD với (

Câu hỏi
Nhận biếtGọi \(\left( \alpha \right)\) là mặt phẳng qua O và song song với mặt phẳng (BEF). Gọi P là giao điểm của SD với \(\left( \alpha \right)\). Tính tỉ số \(\frac{{SP}}{{SD}}\).
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
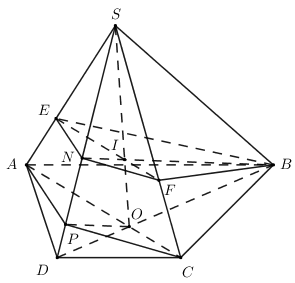
Ta có AC qua O và AC // EF \(\Rightarrow AC \subset \left( \alpha \right)\).
Trong (SAD) qua A kẻ \(AP//EN\,\,\left( {P \in SD} \right) \Rightarrow AP//\left( {BEF} \right) \Leftrightarrow AP \subset \left( \alpha \right)\).
Khi đó ta có \(\left( \alpha \right) \equiv \left( {BEF} \right)\).
Ta có
\(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBD} \right) = OP\\\left( {BEF} \right) \cap \left( {SBD} \right) = BN\\\left( \alpha \right)//\left( {BEF} \right)\end{array} \right. \Rightarrow OP//BN\).
Áp dụng định lí Ta-lét ta có : \(\frac{{DP}}{{DN}} = \frac{{DO}}{{DB}}\).
Ta có : \(\frac{{DO}}{{OB}} = \frac{{DC}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{DO}}{{DB}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{DN}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{PN}} = \frac{1}{2} \Rightarrow DP = \frac{1}{2}NP\).
Lại áp dụng định lí Ta-lét ta có :
\(\begin{array}{l}\frac{{SN}}{{SP}} = \frac{{SE}}{{SA}} = \frac{2}{3}\,\,\left( {AP//EN} \right) \Rightarrow \frac{{SN}}{{NP}} = 2 \Rightarrow SN = 2NP\\\Rightarrow \frac{{SP}}{{SD}} = \frac{{SN + NP}}{{SN + NP + DP}} = \frac{{2NP + NP}}{{2NP + NP + \frac{1}{2}NP}} = \frac{{3NP}}{{\frac{7}{2}NP}} = \frac{6}{7}\end{array}\)
Vậy \(\frac{{SP}}{{SD}} = \frac{6}{7}\).









