Hình thang ABCD có đáy AB = 2CD trong đó A B thuộc trục hoành C D thuộc đồ thị hàm số y = cos x. Biế

Câu hỏi
Nhận biếtHình thang ABCD có đáy AB = 2CD, trong đó A, B thuộc trục hoành, C, D thuộc đồ thị hàm số y = cos x. Biết đường cao của hình thang ABCD bằng \(\frac{{\sqrt 3 }}{2}\) và \(AB < \pi \). Tính độ dài cạnh đáy AB?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
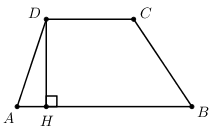
Vẽ \(DH \bot AB\,\,\left( {H \in AB} \right)\) ta có \(DH = \frac{{\sqrt 3 }}{2}\).
Phương trình CD: \(y = \pm \frac{{\sqrt 3 }}{2}\) .
TH1: Phương trình CD: \(y = \frac{{\sqrt 3 }}{2}\) .
Khi đó tọa độ điểm C, D là nghiệm của phương trình .
\(\begin{array}{l}\cos x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + m2\pi \\x = - \frac{\pi }{6} + n2\pi \end{array} \right.\,\,\left( {m,n \in Z} \right)\\\Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{\pi }{6} + m2\pi + \frac{\pi }{6} - n2\pi } \right| = \left| {\frac{\pi }{3} + \left( {m - n} \right)2\pi } \right|\\\Rightarrow \frac{\pi }{3} + \left( {m - n} \right)2\pi < \frac{\pi }{2} \Leftrightarrow \frac{1}{3} + 2\left( {m - n} \right) < \frac{1}{2} \Leftrightarrow m - n < \frac{1}{{12}}
\end{array}\)
Chọn \(m - n = 0 \Leftrightarrow CD = \frac{\pi }{3} \Rightarrow AB = \frac{{2\pi }}{3}\).
TH2 : Phương trình CD \(y = -\frac{{\sqrt 3 }}{2}\) : Tọa độ của C, D là nghiệm của phương trình
\(\cos x = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}
x = \frac{{5\pi }}{6} + m'2\pi \\x = - \frac{{5\pi }}{6} + n'2\pi
\end{array} \right.\,\,\left( {m',n' \in Z} \right)\).
\(\begin{array}{l}\Rightarrow CD = \left| {{x_C} - {x_D}} \right| = \left| {\frac{{3\pi }}{2} + \left( {m' - n'} \right)2\pi } \right|\\Khi\,\,m' - n' = 0 \Rightarrow CD = \frac{{3\pi }}{2} > \frac{\pi }{2}\,\,\left( {ktm} \right)\\Khi\,\,m' - n' = - 1 \Rightarrow CD = \frac{\pi }{2} = \frac{\pi }{2}\,\,\left( {ktm} \right)\end{array}\)
Vậy \(AB = \frac{{2\pi }}{3}\).
Chọn A.









