Cho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy AB CD. Gọi I J lần lượt là trung đi

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm tam giác SAB. Điều kiện nào của AB và CD để thiết diện của hình chóp khi cắt bởi mặt phẳng (IJG) là hình bình hành?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
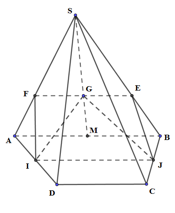
Qua G dựng EF song song AB (\(E \in SB,F \in SA\))
IJ là đường trung bình của hình thang ABCD \( \Rightarrow \left\{ \begin{array}{l}IJ//AB//CD\\IJ = \dfrac{{AB + CD}}{2}\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}IJ//AB\\AB//EF\end{array} \right. \Rightarrow IJ//EF \Rightarrow I,J,E,F\) đồng phẳng
\( \Rightarrow I,J,E,F,G\) đồng phẳng
\( \Rightarrow \left( {GIJ} \right) \equiv \left( {IJEF} \right)\)
Thiết diện của \(\left( {GIJ} \right)\) với hình chóp là hình thang \(IJEF,\,\left( {IJ//EF} \right)\)
Để thiết diện là hình bình hành thì \(IJ = EF\)\( \Leftrightarrow \dfrac{{AB + CD}}{2} = \dfrac{2}{3}AB\) (do \(\dfrac{{EF}}{{AB}} = \dfrac{{SE}}{{SB}} = \dfrac{{SG}}{{SM}} = \dfrac{2}{3}\))
\( \Leftrightarrow 3AB + 3CD = 4AB \Leftrightarrow AB = 3CD\)
Chọn: D









