Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC v

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và \(AB = 2DC\). Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tỉ số \(\dfrac{{GH}}{{GD}}\) bằng:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
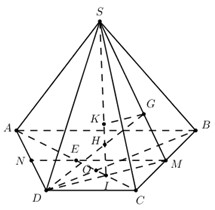
Gọi M là trung điểm của BC, \(I = AC \cap DM\). Trong (SDM) gọi \(H = DG \cap SI\) ta có:
\(\begin{array}{l}I \in AC \Rightarrow I \in \left( {SAC} \right) \Rightarrow SI \subset SAC\\H \in SI \Rightarrow H \in \left( {SAC} \right) \Rightarrow H = DG \cap \left( {SAC} \right)\end{array}\).
Gọi N là trung điểm của AD, \(E = AC \cap MN\) \( \Rightarrow MN\) là đường trung bình của hình thang ABCD \( \Rightarrow MN//AB//CD\) và \(MN = \dfrac{{AB + CD}}{2} = \dfrac{{2CD + CD}}{2} = \dfrac{{3CD}}{2}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{NE}}{{CD}} = \dfrac{{AN}}{{AD}} = \dfrac{1}{2} \Rightarrow NE = \dfrac{1}{2}CD \Rightarrow ME = \dfrac{3}{2}CD - \dfrac{1}{2}CD = CD\)
\(\dfrac{{IM}}{{ID}} = \dfrac{{CD}}{{MN}} = \dfrac{{ME}}{{CD}} = 1 \Rightarrow IM = ID\).
Kẻ \(GK//DM\), áp dụng định lí Vi-ét ta có : \(\dfrac{{GH}}{{DH}} = \dfrac{{KG}}{{ID}} = \dfrac{{KG}}{{IM}} = \dfrac{{KG}}{{IM}} = \dfrac{{SG}}{{SM}} = \dfrac{2}{3}\)
\( \Rightarrow \dfrac{{GH}}{{GH + DH}} = \dfrac{2}{{2 + 3}} = \dfrac{2}{5} \Rightarrow \dfrac{{GH}}{{GD}} = \dfrac{2}{5}\).
Chọn C.









