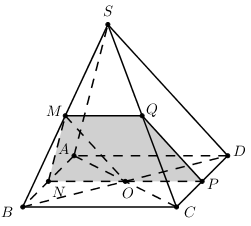
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M N lần lượt là trung điểm SB AB. Thiế

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SB, AB. Thiết diện tạo bởi mặt phẳng (OMN) và hình chóp S.ABCD là hình gì ?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Trong (ABCD) gọi \(P = NO \cap CD\).
(OMN) và (SBC) có điểm M chung ; ON // BC \( \Rightarrow \) Giao tuyến của (OMN) và (ABCD) là đường thẳng qua M và song song với BC và ON.
Trong (SBC), qua M kẻ \(MQ//BC\,\,\left( {Q \in SC} \right)\).
Vậy thiết diện là MNPQ là hình thang.
Chọn B.