Cho tứ diện ABCD. Gọi I J lần lượt thuộc các cạnh AD BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặ

Câu hỏi
Nhận biếtCho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Thiết diện của mặt phẳng (P) và tứ diện ABCD là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
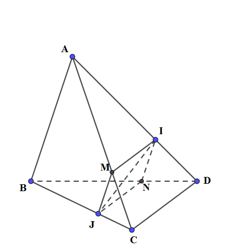
Kẻ MJ // AB, \(M \in AC\); NI // AB \(N \in BD\) \( \Rightarrow M,N,I,J\) đồng phẳng và \(\left( {MINJ} \right) \equiv \left( P \right)\)
Thiết diện của mặt phẳng (P) và tứ diện ABCD là tứ giác MINJ, có:
\(MJ//NI\) và \(MJ = IN\) (do \(\frac{{MJ}}{{AB}} = \frac{{JC}}{{BC}} = \frac{1}{3},\,\,\frac{{IN}}{{AB}} = \frac{{ND}}{{BD}} = \frac{1}{3}\))
\( \Rightarrow MINJ\) là hình bình hành.
Chọn: B









