Cho hình chóp S.ABCD có ABCD là hình thang đáy lớn BC với BC = 2aAD = AB = a mặt bên ( SAD )là tam g

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang, đáy lớn BC với \(BC = 2a,\,\,AD = AB = a\), mặt bên \(\left( {SAD} \right)\)là tam giác đều. Lấy điểm \(M\) trên cạnh AB sao cho \(MB = 2AM\). Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC. Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng \(\left( \alpha \right)\) và tính diện tích của thiết diện đó.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
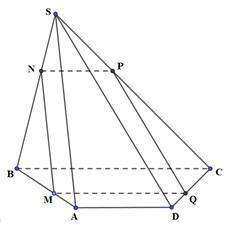
* Dựng thiết diện:
Qua M kẻ MQ song song BC (\(Q \in DC\)), kẻ MN song song SA (\(N \in SB\))
Qua N kẻ NP song song BC (\(P \in SC\))
Khi đó, \(\left( {MNPQ} \right)\) là mặt phẳng qua M và song song BC, SA
\( \Rightarrow \left( {MNPQ} \right) \equiv \left( \alpha \right)\)
Thiết diện của hình chóp bị cắt bởi mặt phẳng \(\left( \alpha \right)\) là tứ giác \(MNPQ\).
* Tính diện tích thiết diện:
Ta có: NP // MQ (cùng song song BC) \( \Rightarrow MNPQ\) là hình thang
\(\Delta SAD\) đều \( \Rightarrow SA = SD = AD = a\)
ABCD là hình thang, \(MQ//BC \Rightarrow \dfrac{{CQ}}{{DC}} = \dfrac{{BM}}{{AB}} = \dfrac{{BN}}{{SB}} = \dfrac{2}{3}\)
\(MN//SA \Rightarrow \dfrac{{MN}}{{SA}} = \dfrac{{BM}}{{AB}} = \dfrac{2}{3} \Rightarrow MN = \dfrac{2}{3}SA = \dfrac{2}{3}a\)
\(NP//BC \Rightarrow \dfrac{{NP}}{{BC}} = \dfrac{1}{3} \Rightarrow NP = \dfrac{1}{3}.BC = \dfrac{2}{3}a\) và \(\dfrac{{PC}}{{SC}} = \dfrac{{NB}}{{SB}} = \dfrac{2}{3} \Rightarrow \dfrac{{PC}}{{SC}} = \dfrac{{CQ}}{{DC}} = \dfrac{2}{3} \Rightarrow \dfrac{{PQ}}{{SD}} = \dfrac{2}{3} \Rightarrow PQ = \dfrac{2}{3}SD = \dfrac{2}{3}a\)
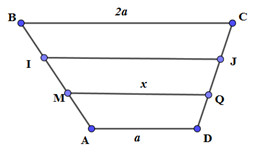
Gọi I, J lần lượt là trung điểm của BM, CQ.
Giả sử MQ có độ dài bằng x. Khi đó, do IJ là đường trung bình của hình thang BCQM \( \Rightarrow IJ = \dfrac{{MQ + BC}}{2} = \dfrac{{x + 2a}}{2}\)
Do MQ là đường trung bình của hình thang IJDA \(\begin{array}{l} \Rightarrow 2MQ = IJ + AD \Leftrightarrow 2x = \dfrac{{x + 2a}}{2} + a \Leftrightarrow 4x = x + 2a + 2a \Leftrightarrow x = \dfrac{4}{3}a\\ \Rightarrow MQ = \dfrac{4}{3}a\end{array}\)
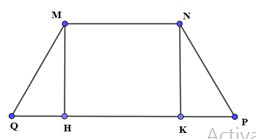
Xét hình thang MNPQ có: \(NP = MN = PQ = \dfrac{2}{3}a,\,\,MQ = \dfrac{4}{3}a\)\( \Rightarrow MNPQ\) là hình thang cân.
Kẻ MH, NK vuông góc PQ (H, K thuộc PQ)
\( \Rightarrow QH = PK = \dfrac{{PQ - MN}}{2} = \dfrac{{\dfrac{4}{3}a - \dfrac{2}{3}a}}{2} = \dfrac{a}{3}\)
\( \Rightarrow MH = \sqrt {M{Q^2} - Q{H^2}} = \sqrt {{{\left( {\dfrac{2}{3}a} \right)}^2} - {{\left( {\dfrac{1}{3}a} \right)}^2}} = \sqrt {\dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 3 }}{3}\)
Diện tích hình thang MNPQ: \(S = \dfrac{1}{2}\left( {MN + PQ} \right).MH = \dfrac{1}{2}.\left( {\dfrac{2}{3}a + \dfrac{4}{3}a} \right).\dfrac{{a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 3 }}{3}\).









