Có bao nhiêu số nguyên m để phương trình sin 2x - 2 căn 2 (sin x + cos x) = m có nghiệm?

Câu hỏi
Nhận biếtCó bao nhiêu số nguyên m để phương trình \(\sin 2x - 2\sqrt 2 (\sin x + \cos x) = m\) có nghiệm?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Đặt \(\sin x + \cos x = t = \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = \sqrt 2 \cos \left( {\frac{\pi }{4} - x} \right)\)\(\left( { - \sqrt 2 \le t \le \sqrt 2 } \right).\) \( \Rightarrow \sin x\cos x = \frac{{{t^2} - 1}}{2}\)
Khi đó phương trình trở thành \(\left( {{t^2} - 1} \right) - 2\sqrt 2 t = m \Leftrightarrow {t^2} - 2\sqrt 2 t - 1 = m\,\,\,\left( * \right)\).
Để phương trình ban đầu có nghiệm x thì phương trình \(\left( * \right)\) có nghiệm \(t \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\)
Xét \(f\left( t \right) = {t^2} - 2\sqrt 2 t - 1 = {\left( {t - \sqrt 2 } \right)^2} - 3\) trên \( - \sqrt 2 \le t \le \sqrt 2 \)
BBT:
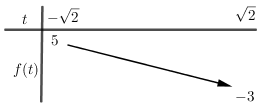
Để phương trình có nghiệm thì \(m \in \left[ { - 3;5} \right]\). Các giá trị nguyên của m: \(m \in \left\{ { - 3; - 2; - 1;0;1;...;5} \right\}\); có 9 giá trị nguyên của m.
Chọn B.









