Cho tam giác ABC có diện tích 12cm^2 . Gọi N là trung điểm của BC M trên AC sao cho AM=13AC AN cắt
Câu hỏi
Nhận biếtCho tam giác ABC có diện tích \(12c{{m}^{2}}\) . Gọi N là trung điểm của BC, M trên AC sao cho \(AM=\frac{1}{3}AC\) , AN cắt BM tại O
a) Chứng minh rằng \(AO=ON\)
b) Chứng minh rằng \(BO=3OM\)
c) Tính diện tích tam giác AOM
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
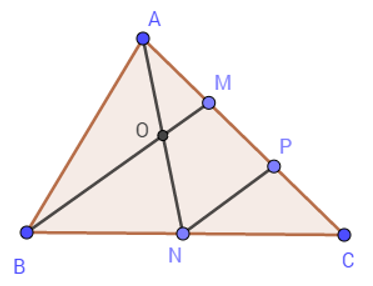
a) Lấy P là trung điểm của CM.
Tam giác BCM có: \(\left\{ \begin{align} & NB=NC\,\,(gt) \\ & PC=PM\,\,(gt) \\ \end{align} \right.\)
Suy ra NP là đường trung bình của tam giác BMC (định nghĩa).
Suy ra \(NP\parallel BM\) (tính chất đường trung bình).
Tam giác ANP có \(\left\{ \begin{align} & MA=MP\,\,\,(gt) \\ & OM\parallel NP\,\,\,(do\,\,NP\parallel BM) \\ \end{align} \right.\)
\(\Rightarrow AO=ON\) (định lý đảo của đường trung bình).
b) Theo a) ta có OM là đường trung bình của tam giác ANP nên \(OM=\frac{1}{2}NP\,\,\,\,(1)\)
NP là đường trung bình của tam giác BCM nên \(NP=\frac{1}{2}BM\,\,\,(2)\)
Từ (1) và (2) suy ra \(BM=4OM\Rightarrow BO=3OM\) .
c) Hai tam giác AOM và ABM có chung đường cao hạ từ A nên \(\frac{{{S}_{AOM}}}{{{S}_{ABM}}}=\frac{OM}{BM}=\frac{1}{4}\Rightarrow {{S}_{AOM}}=\frac{1}{4}{{S}_{ABM}}\)
Hai tam giác ABM và ABC có chung đường cao hạ từ B nên \(\frac{{{S}_{ABM}}}{{{S}_{ABC}}}=\frac{AM}{AC}=\frac{1}{3}\Rightarrow {{S}_{ABM}}=\frac{1}{4}{{S}_{ABC}}\)
Vậy \({{S}_{AOM}}=\frac{1}{4}.\frac{1}{3}.12=1\left( c{{m}^{2}} \right)\)
Chọn A
Luyện tập
Câu hỏi liên quan
-
Tính giá trị của biểu thức \(B = \left( {x + 5} \right)\left( {x - 5} \right) - {x^2} + 7\left( {x - 5} \right)\) tại x = 1:
-
Tìm x biết:
\(a)\;{x^2} - 3x - 10 = 0\) \(b)\;7x\left( {3x - 2} \right) - 4 + 6x = 0\)
-
Cho tứ giác ABCD, lấy N, M, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác NMPQ là hình gì?
-
Kết quả của phép tính \(\left( {3x + 1} \right)\left( {9{x^2} - 3x + 1} \right)\) bằng:
-
Biểu thức \(C = {13^{n + 2}} - {13^n}.23\) (với n là số tự nhiên bất kì) luôn chia hết cho số tự nhiên nào dưới đây?
-
Hãy chọn câu đúng. Hình bình hành ABCD là hình chữ nhật khi:
-
Rút gọn:
\(P = {{\left( {x + 1} \right)\left( {4{x^2} - 4x + 1} \right) + \left( {x - 1} \right)\left( {4{x^2} - 4x + 1} \right)} \over {\left( {x + 3} \right)\left( {x - 1} \right) - {x^2} - 1}}\) (với \(\left( {2x - 1} \right) \ne 0\) )
-
Rút gọn biểu thức \(A = {{\left( {9{x^2} + 12x + 4} \right).\left( {3x - 2} \right)} \over {\left( {3x + 2} \right)}}\)
-
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
-
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng: