Cho hình thang cân MNPQ. Gọi A B C D lần lượt là trung điểm của MN NP PQ PM. Tứ giác ABCD là hình g

Câu hỏi
Nhận biếtCho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là trung điểm của MN, NP, PQ, PM. Tứ giác ABCD là hình gì?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
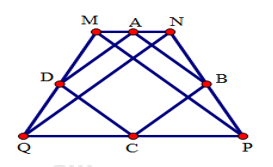
Do MNPQ là hình thang cân nên MP = NQ. (hình thang cân có hai đường chéo bằng nhau).
Do A, D lần lượt là trung điểm của MN, MQ nên AD là đường trung bình của tam giác MNQ. Do đó \(DA = {1 \over 2}QN\) (1) (tính chất đường trung bình của tam giác). (2)
Chứng minh tương tự ta cũng có BC, AB, DC lần lượt là đường trung bình của các tam giác PQN, MNP, QMP.
Do đó \(BC = {1 \over 2}QN;\,\,AB = {1 \over 2}MP;\,\,DC = {1 \over 2}MP\,\,\,\,\left( 3 \right)\)
Từ (1), (2), (3) suy ra AB = BC = CD = DA.
Do đó ABCD là hình thoi.
Chọn D
Luyện tập
Câu hỏi liên quan
-

Rút gọn biểu thức \(A = {{\left( {9{x^2} + 12x + 4} \right).\left( {3x - 2} \right)} \over {\left( {3x + 2} \right)}}\)
-

Tìm x biết:
\(a)\;{x^2} - 3x - 10 = 0\) \(b)\;7x\left( {3x - 2} \right) - 4 + 6x = 0\)
-

Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
-

Tính giá trị của biểu thức \(B = \left( {x + 5} \right)\left( {x - 5} \right) - {x^2} + 7\left( {x - 5} \right)\) tại x = 1:
-

Rút gọn:
\(P = {{\left( {x + 1} \right)\left( {4{x^2} - 4x + 1} \right) + \left( {x - 1} \right)\left( {4{x^2} - 4x + 1} \right)} \over {\left( {x + 3} \right)\left( {x - 1} \right) - {x^2} - 1}}\) (với \(\left( {2x - 1} \right) \ne 0\) )
-

Cho tứ giác ABCD, lấy N, M, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác NMPQ là hình gì?
-

Kết quả của phép tính \(\left( {3x + 1} \right)\left( {9{x^2} - 3x + 1} \right)\) bằng:
-

Hãy chọn câu đúng. Hình bình hành ABCD là hình chữ nhật khi:
-

Biểu thức \(C = {13^{n + 2}} - {13^n}.23\) (với n là số tự nhiên bất kì) luôn chia hết cho số tự nhiên nào dưới đây?
-

Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
