Cho G là trọng tậm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.
Câu hỏi
Nhận biếtCho G là trọng tậm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
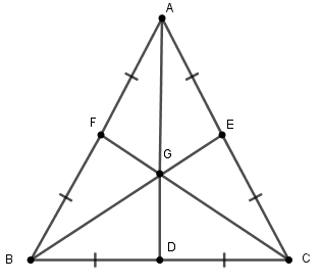
Các tia AG, BG và CG cắt BC, AC, AB lần lượt tại D, E, F thì D, E, F theo thứ tự là trung điểm của BC, AC, AB.
Mà BC = AC = AB (Do tam giác ABC là tam giác đều), do đó BD = DC = CE = EA = AF = FB
Xét \(\Delta AEB\) và \(\Delta AFC\) ta có: AB = AC; \(\widehat{A}\)chung; AE = AF.
Vậy \(\Delta AEB=AFC\,(c.g.c)\), suy ra BE = CF (1)
Chứng minh tương tự ta có \(\Delta BEC=ADC\,(c.g.c)\), suy ra BE = AD (2)
Từ (1) và (2) ta có: AD = BE = CF (3)
Theo đề bài G là trọng tậm của tam giác ABC nên ta có:
\(GA=\frac{2}{3}AD;\,\,GB=\frac{2}{3}BE;\,\,GC=\frac{2}{3}CF\)
Vì thế từ (3) ta suy ra GA = GB = GC.
Luyện tập
Câu hỏi liên quan
-
Số điểm \(10\) trong kì kiểm tra học kì I của ba bạn Tài, Thảo, Ngân tỉ lệ với \(3;1;2\). Số điểm \(10\) của cả ba bạn đạt được là \(24\). Số điểm \(10\) của bạn Ngân đạt được là
-
Tìm x biết:
a) \(1{2 \over 5}x + {3 \over 7} = - {4 \over 5}\)
b) \({\left( {{x} + {1 \over 3}} \right)^3} = \left( {{{ - 1} \over 8}} \right)\)
c) \(\left| {x + {2 \over 3}} \right| + 2 = 2{1 \over 3}\)
-
Ba vời nước cùng chảy vào một hồ có dung tích \(15,8{{m}^{3}}\) từ lúc hồ không có nước cho tới khi đầy hồ. Biết rằng thời gian để chảy được \(1{{m}^{3}}\) nước của vòi thứ nhất là \(3\) phút, vòi thứ hai là \(5\) phút và vòi thứ ba là \(8\) phút. Hỏi mỗi vời chảy được bao nhiêu nước vào hồ?
-
Tìm các số \(x,y\) biết:
a.\(\frac{x}{5}=\frac{y}{7}\) và \(xy=140\)
b.\(\frac{x}{-3}=\frac{y}{8}\) và \({{x}^{2}}-{{y}^{2}}=\frac{-44}{5}\)
-
Tìm x , biết : \(x:{\left( { - 2} \right)^5} = {\left( { - 2} \right)^3}\) Kết quả x bằng :
-
Kết qủa của phép tính \({3 \over 4} + {1 \over 4}:{{12} \over {20}}\) là
-
Giá trị của x trong phép tính \({3 \over 4} - x = {1 \over 3}\) là:
-
Tìm các số tự nhiên x, y biết: \({2^{x + 1}}{.5^y} = {20^x}\)
-
Cho \(\left| x \right| = 2\) thì :
-
Tìm \(x, y, z\) biết:
a) \(x + 1 = - 2\)
b) \(x:2 = 10:5\)
c) \({\rm{x:2 = y:3}}\) và\({\rm{x + y = 10}}\)
d) \(3x = 2y; 7y = 5z\) và \(x – y + z = 32\)