Cho ∆ ABC vuông tại A , gọi M là trung điểm của AC . Gọi D là điểm đ
Câu hỏi
Nhận biếtCho \(\Delta ABC\) vuông tại \(A\) , gọi \(M\) là trung điểm của \(AC\) . Gọi \(D\) là điểm đối xứng với \(B\) qua \(M\) .
a. Chứng minh tứ giác \(ABC{\rm{D}}\) là hình bình hành.
b. Gọi \(N\) là điểm đối xứng với \(B\) qua \(A\) . Chứng minh tứ giác \(AC{\rm{D}}N\) là hình chữ nhật.
c. Kéo dài \(MN\) cắt \(BC\) tại \(I\) . Vẽ đường thẳng qua \(A\) song song với \(MN\) cắt \(BC\) ở \(K\) . Chứng minh: \(KC = 2BK\)
d. Qua \(B\) kẻ đường thẳng song song với \(MN\) cắt \(AC\) kéo dài tại \(E\) . Tam giác \(ABC\) cần có thêm điều kiện gì để tứ giác \(EBMN\) là hình vuông.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
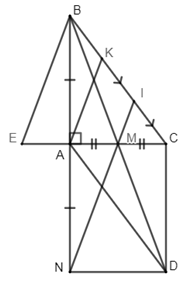
a. Ta có: Vì \(D\) và \(B\) đối xứng với nhau qua \(M\) (gt) \( \Rightarrow M{\rm{D}} = MB\)(tính chất hai điểm đối xứng với nhau qua 1 điểm)
Xét tứ giác \(ABC{\rm{D}}\) ta có: \(\left\{ \begin{array}{l}MC = MA\left( {gt} \right)\\M{\rm{D}} = MB\left( {cmt} \right)\end{array} \right.\)
\( \Rightarrow \) Tứ giác \(ABC{\rm{D}}\) là hình bình hành (dhnb)
b. Vì \(N\) đối xứng với \(B\) qua \(A\) (gt)
\( \Rightarrow NA = AB\)(tính chất)
Lại có \(ABC{\rm{D}}\) là hình bình hành (cmt)
\( \Rightarrow \left\{ \begin{array}{l}DC = AB\\DC//AB\end{array} \right.\)(tính chất) \( \Rightarrow \left\{ \begin{array}{l}DC = AN\\DC//AN\end{array} \right.\)
\( \Rightarrow AN{\rm{D}}C\) là hình bình hành (dhnb)
Mặt khác, \(\angle CAB = {90^0}\left( {gt} \right) \Rightarrow \angle CAN = {90^0}\)
\( \Rightarrow \) hình bình hành \(AN{\rm{D}}C\) là hình chữ nhật (dhnb) (đpcm)
c. Xét \(\Delta BNI\) có: \(AK//NI\) (do \(AK//MN\) )
\(NA = AB\left( {gt} \right)\)
\( \Rightarrow \) \(AK\) là đường trung bình của \(\Delta BNI\)(định lý)
\( \Rightarrow KI = KB\) (tính chất)
Xét \(\Delta CAK\) có: \(MI//AK\) (do \(AK//NI\))
\(MA = MC\) (gt)
\( \Rightarrow \) \(MI\) là đường trung bình của \(\Delta ACK\) (dhnb)
\( \Rightarrow IK = CI\) (tính chất)
Mà \(KC = CI + IK \Rightarrow KC = 2KI = 2KB\) (do \(KI = KB\))
d. Vì \(BE//MN\left( {gt} \right) \Rightarrow BE//IM \Rightarrow \) Tứ giác \(BEMI\) là hình thang (dấu hiệu nhận biết hình thang)
Lại có: K là trung điểm của BI (cmt) và \(AK//MI\left( {cmt} \right) \Rightarrow A\)là trung điểm của EM (trong hình thang, nếu một đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì đi qua trung điểm của cạnh bên thứ hai)
Xét tứ giác \(BENM\) có hai đường chéo BN và EM cắt nhau tại trung điểm A của mỗi đường.
\( \Rightarrow BENM\)là hình bình hành (dhnb)
Mà \(BN \bot EM\left( {gt} \right) \Rightarrow \) hình bình hành BENM là hình thoi (dhnb)
Để hình thoi BENM là hình vuông khi và chỉ khi \(AB = AM \Leftrightarrow AB = \frac{1}{2}AC\).
Luyện tập
Câu hỏi liên quan
-
Biểu thức \(C = {13^{n + 2}} - {13^n}.23\) (với n là số tự nhiên bất kì) luôn chia hết cho số tự nhiên nào dưới đây?
-
Tính giá trị của biểu thức \(B = \left( {x + 5} \right)\left( {x - 5} \right) - {x^2} + 7\left( {x - 5} \right)\) tại x = 1:
-
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
-
Rút gọn biểu thức \(A = {{\left( {9{x^2} + 12x + 4} \right).\left( {3x - 2} \right)} \over {\left( {3x + 2} \right)}}\)
-
Tìm x biết:
\(a)\;{x^2} - 3x - 10 = 0\) \(b)\;7x\left( {3x - 2} \right) - 4 + 6x = 0\)
-
Rút gọn:
\(P = {{\left( {x + 1} \right)\left( {4{x^2} - 4x + 1} \right) + \left( {x - 1} \right)\left( {4{x^2} - 4x + 1} \right)} \over {\left( {x + 3} \right)\left( {x - 1} \right) - {x^2} - 1}}\) (với \(\left( {2x - 1} \right) \ne 0\) )
-
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
-
Kết quả của phép tính \(\left( {3x + 1} \right)\left( {9{x^2} - 3x + 1} \right)\) bằng:
-
Cho tứ giác ABCD, lấy N, M, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác NMPQ là hình gì?
-
Hãy chọn câu đúng. Hình bình hành ABCD là hình chữ nhật khi: