Cho tam giác ABC biết $A\left( { - 1;\,\,2} \right),\,\,B\left( {2;\,\,0} \right),\,\,C\left( { - 3;\,\,1} \right)$. Tìm tọa độ điểm M thuộc BC sao cho ${S_{ABM}} = \dfrac{1}{3}{S_{ABC}}$.
Phương pháp giải
Tham số hóa tọa độ điểm M, sử dụng công thức tính diện tích tam giác và biểu diễn tọa độ các vector
Lời giải của Tự Học 365
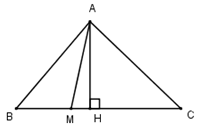
Giả sử M(x; y) là điểm thỏa mãn điều kiện đề bài.
Kẻ AH vuông góc với BC. Suy ra
$\begin{array}{l}\dfrac{1}{2}BM.AH = \dfrac{1}{3}.\dfrac{1}{2}AH.BC \Rightarrow \overrightarrow {BM} = \dfrac{1}{3}\overrightarrow {BC} \\\left( {x - 2;y} \right) = \dfrac{1}{3}\left( { - 5;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x - 2 = - \dfrac{5}{3}\\y = \dfrac{1}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{3}\\y = \dfrac{1}{3}\end{array} \right. \Rightarrow M\left( {\dfrac{1}{3};\dfrac{1}{3}} \right).\end{array}$
Đáp án cần chọn là: d
Toán Lớp 12
