Câu hỏi
Vận dụng
Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\); \(I\) là trung điểm của \(AD\) . Khi đó \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \) bằng:
Đáp án đúng: b
Phương pháp giải
Để ý \(\overrightarrow {AB} .\overrightarrow {ID} = 0\) nên xen điểm \(A\) vào giữa hai điểm \(I\) và \(B\)
Lời giải của Tự Học 365
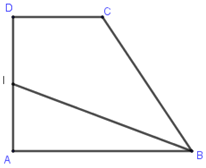
Ta có \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} = \left( {\overrightarrow {IA} + \overrightarrow {IA} + \overrightarrow {AB} } \right).\overrightarrow {ID} = 2\overrightarrow {IA} .\overrightarrow {ID} = - \dfrac{{9{a^2}}}{2}\) nên chọn B.
Đáp án cần chọn là: b
Toán Lớp 12
