Câu hỏi
Thông hiểu
Cho hình chóp \(S.ABC\) có \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng \(SA\) và \(BC.\)
Đáp án đúng: d
Phương pháp giải
Dựa vào các điều kiện bài cho tìm mối quan hệ góc, độ dài của các cạnh hình chóp, từ đó suy ra góc giữa hai đường thẳng.
Lời giải của Tự Học 365
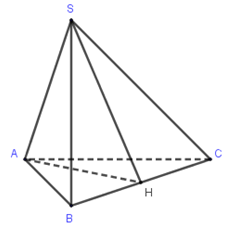
Vì \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\) nên \(\Delta \,SAC = \Delta \,SAB\), suy ra \(SB = SC\), nên hai tam giác \(ABC\) và \(SBC\) là tam giác cân. Gọi \(H\) là trung điểm \(BC\), ta có \(\left\{ \begin{array}{l}AH \bot BC\\SH \bot BC\end{array} \right. \Rightarrow \left( {SAH} \right) \bot BC\).
Vậy \(SA \bot BC\).
Đáp án cần chọn là: d
Toán Lớp 12
