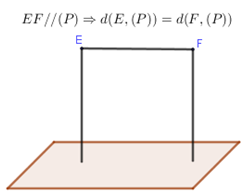
Lời giải của Tự Học 365

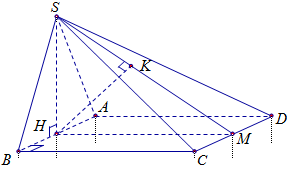
Gọi \(H\), \(M\) lần lượt là trung điểm của \(AB\) và \(CD\) suy ra \(HM = 1\), \(SH = \dfrac{{\sqrt 3 }}{2}\) và \(SM = \dfrac{{\sqrt 7 }}{2}\)

Vì tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy \(\left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).

Vì \(AB{\rm{//C}}D\) nên \(AB{\rm{//}}\left( {SCD} \right)\).

Do đó \(d\left( {B;\,\left( {SCD} \right)} \right) = d\left( {H;\,\left( {SCD} \right)} \right) = HK\) với \(HK \bot SM\) trong \(\Delta SHM\).

Ta có:\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{M^2}}}\)\( \Rightarrow HK = \dfrac{{\sqrt {21} }}{7}\).

Đáp án cần chọn là: d