Lời giải của Tự Học 365

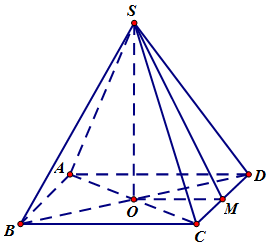
Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp \(S.ABCD\) là hình chóp đều \( \Rightarrow \left\{ \begin{array}{l}SO \bot (ABCD)\\AC \bot BD\end{array} \right.\).

Do M là trung điểm của CD nên ta có:

\(\overrightarrow {MS}  = \overrightarrow {{\rm{O}}S}  - \overrightarrow {OM}  =  - \dfrac{1}{2}\overrightarrow {OC}  - \dfrac{1}{2}\overrightarrow {OD}  + \overrightarrow {{\rm{O}}S} \), \(\overrightarrow {CB}  = \overrightarrow {OB}  - \overrightarrow {OC}  =  - \overrightarrow {OD}  - \overrightarrow {OC} \).

Do \(\overrightarrow {OC} ;\) \(\overrightarrow {OS} ;\) \(\overrightarrow {OD} \) đôi một vuông góc với nhau nên ta có:

\(\overrightarrow {MS} .\overrightarrow {CB}  = \dfrac{1}{2}O{C^2} + \dfrac{1}{2}O{D^2} = O{C^2} = \dfrac{{{a^2}}}{2}\)

Đáp án cần chọn là: a