Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Lấy \(N\) trên cạnh \(C'D\) sao cho \(C'N = xC'D\). Với giá trị nào của \(x\) thì \(MN\;{\rm{//}}\;BD'\).
Phương pháp giải
- Tìm một điểm \(N'\) thỏa mãn \(MN'//BD'\)
- Từ đó suy ra \(N \equiv N'\) và kết luận.
Lời giải của Tự Học 365
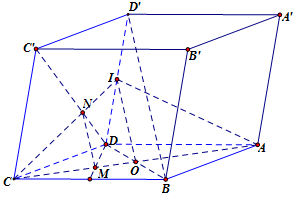
Ta có: \(M\) là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Nên \(M\) là trọng tâm của tam giác \(BCD\).
Gọi \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(DD'\). Khi đó ta có: \(BD'\;{\rm{//}}\;\left( {IAC} \right)\).
Trong \(\left( {CDD'C'} \right)\), gọi \(N' = CI \cap C'D\). Suy ra \(N'\) là trọng tâm tam giác \(CDD'\).
Do đó: \(\dfrac{{CM}}{{CO}} = \dfrac{2}{3} = \dfrac{{CN'}}{{CI}}\) \( \Rightarrow MN'\;{\rm{//}}\;OI\), mà \(OI\;{\rm{//}}\;BD'\) nên \(MN'\;{\rm{//}}\;BD'\).
Vậy \(N' \equiv N\) và \(x = \dfrac{2}{3}\)
Đáp án cần chọn là: a
Toán Lớp 12
