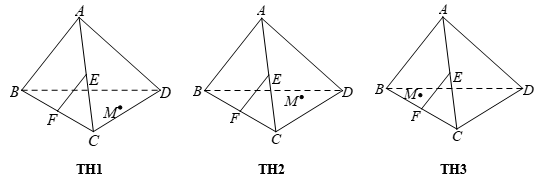
Cho tứ diện \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của các cạnh \(AC\) và \(BC\). Trên mặt phẳng \(\left( {BCD} \right)\) lấy một điểm \(M\) tùy ý (điểm \(M\) có đánh dấu tròn như hình vẽ). Nêu đầy đủ các trường hợp (TH) để thiết diện tạo bởi mặt phẳng \(\left( {MEF} \right)\) với tứ diện \(ABCD\) là một tứ giác.
Phương pháp giải
Xác định thiết diện của tứ diện được cắt bởi mặt phẳng \(\left( {MEF} \right)\) ở mỗi trường hợp và kết luận.
Lời giải của Tự Học 365
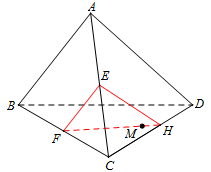
Hình ở TH1: Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(CD\) tại \(H\). Thiết diện là tam giác \(EFH\).
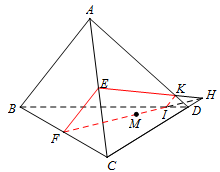
Hình ở TH2:
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
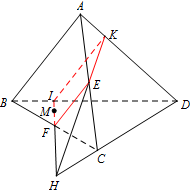
Hình ở TH3:
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
Đáp án cần chọn là: c
Toán Lớp 12
