Cho lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy là một tam giác vuông cân tại \(B\), \(AB = BC = a\), \(AA' = a\sqrt 2 \), \(M\) là trung điểm \(BC\). Tính khoảng cách giữa hai đường thẳng\(AM\) và \(B'C\).
Phương pháp giải
Sử dụng định lý: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này tới mặt phẳng song song với đường thẳng này mà chứa đường thẳng kia.
Cụ thể:
+ Tìm mặt phẳng chứa \(AM\) mà song song với \(B'C\)
+ Tính khoảng cách từ \(B'C\) đến mặt phẳng trên: bằng khoảng cách từ một điểm bất kì thuộc đường thẳng này đến mặt phẳng.
Lời giải của Tự Học 365
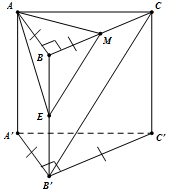
Gọi \(E\) là trung điểm của \(BB'\). Khi đó:$EM{\kern 1pt} \;{\rm{//}}\;B'C$ \( \Rightarrow B'C{\kern 1pt} \;{\rm{//}}\;(AME)\)
Ta có: \(d\left( {AM,B'C} \right) = d\left( {B'C,\left( {AME} \right)} \right) = d\left( {C,\left( {AME} \right)} \right) = d\left( {B,\left( {AME} \right)} \right)\)
Xét khối chóp \(BAME\) có các cạnh \(BE\), \(AB\), \(BM\) đôi một vuông góc với nhau nên
\(\dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{M{B^2}}} + \dfrac{1}{{E{B^2}}}\)\( \Leftrightarrow \dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = 7{a^2}\)\( \Leftrightarrow {d^2}\left( {B,\left( {AME} \right)} \right) = \dfrac{{{a^2}}}{7}\)
\( \Leftrightarrow d\left( {B,\left( {AME} \right)} \right) = \dfrac{a}{{\sqrt 7 }}\).
Đáp án cần chọn là: a
Toán Lớp 12
