Cho tứ diện $ABCD$, $G$ là trọng tâm tứ diện. Gọi \({G_1}\) là giao điểm của $AG$ và mặt phẳng $\left( {BCD} \right)$, \({G_2}\) là giao điểm của $BG$ và mặt phẳng $\left( {ACD} \right)$. Khẳng định nào sau đây là đúng?
Phương pháp giải
- Trọng tâm tứ diện là giao điểm của các đường nối trung điểm các cạnh của tứ diện.
- Xác định vị trí các điểm \({G_1},{G_2}\) và xét tính đúng sai của từng đáp án bằng phương pháp chứng minh hai đường thẳng song song trong hình phẳng (định lý Ta – lét đảo)
Lời giải của Tự Học 365
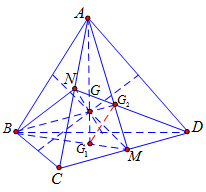
Gọi $M$, $N$ lần lượt là trung điểm của $DC$, $AC$. Vì $G$ là trọng tâm tứ diện nên $G$ là giao điểm của ba đoạn thẳng nối hai trung điểm của cặp cạnh đối của tứ diện như hình vẽ trên.
Xét $\left( {ABM} \right)$: $AG \cap BM = {G_1}$, $BG \cap AM = {G_2}$. Trong $\Delta ACD$ có $AM$ và $DN$ là đường trung tuyến nên \({G_2}\) là trọng tâm của tam giác do đó $\dfrac{{{G_2}M}}{{{G_2}A}} = \dfrac{1}{2}$.
Tương tự ta cũng có $\dfrac{{{G_1}M}}{{{G_1}B}} = \dfrac{1}{2}$ suy ra \({G_1}{G_2}\,{\rm{//}}\,AB\).
Đáp án cần chọn là: a
Toán Lớp 12
