Câu hỏi
Thông hiểu
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), gọi \(I\) là trung điểm cạnh \(SC\). Mệnh đề nào sau đây sai ?
Đáp án đúng: c
Phương pháp giải
Dựng hình, xét tính đúng sai của từng đáp án dựa vào các phương pháp chứng minh đường thẳng song song với mặt phẳng, phương pháp xác định giao tuyến của hai mặt phẳng để kiểm tra.
Lời giải của Tự Học 365
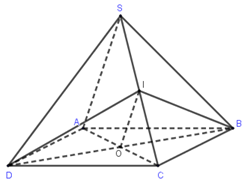
\(IO\) là đường trung bình tam giác \(SAC\) nên \(IO\,\,{\rm{//}}\,\,SA\)\( \Rightarrow IO\,{\rm{//}}\,\left( {SAB} \right)\), \(IO\,\,{\rm{//}}\,\,\left( {SAC} \right)\). Do đó A, B đúng.
\(I \in SC\), \(O = AC \cap BD\)\( \Rightarrow \left( {IBD} \right) \cap \left( {SAC} \right) = IO\) nên D đúng.
Đáp án cần chọn là: c
Toán Lớp 12
