Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật. Mặt phẳng \(\left( P \right)\) cắt các cạnh \(SA\), \(SB\), \(SC\), \(SD\) lần lượt tại $M$, \(N\), \(P\), \(Q\) . Gọi \(I\) là giao điểm của \(MQ\) và \(NP\). Câu nào sau đây đúng?
Phương pháp giải
Sử dụng định lý ba giao tuyến để tìm điểm \(I\) rồi từ đó kiểm tra tính đúng sai của từng đáp án.
Lời giải của Tự Học 365
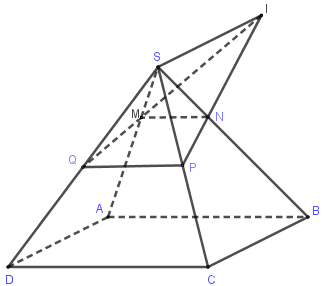
Xét ba mặt phẳng \(\left( {MNPQ} \right),\left( {SAD} \right),\left( {SCB} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAD} \right) = MQ\\\left( {MNPQ} \right) \cap \left( {SBC} \right) = NP\\\left( {SAD} \right) \cap \left( {SBC} \right) = d\end{array} \right.\)
Mà \(MQ \cap NP = I\) nên \(d\) đi qua \(I\) hay giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) chính là \(SI\)
Ngoài ra, ta đã biết giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) là đường thẳng đi qua \(S\) và song song với \(AD,BC\)
Vậy \(SI//AD//BC\)
Đáp án cần chọn là: c
Toán Lớp 12
