Trong không gian với hệ tọa độ ${\rm{Ox}}yz$, mặt phẳng \(\left( \alpha \right)\) chắn các trục $Ox,\,\,Oy,\,\,Oz$ lần lượt tại $A,\,\,B,\,\,C$ sao cho $H\left( {3;\,\, - 4;\,\,2} \right)$ là trực tâm của tam giác \(ABC\). Phương trình mặt phẳng \(\left( \alpha \right)\) là
Phương pháp giải
Mặt phẳng cần tìm đi qua \(H\) và vuông góc với \(\overrightarrow {OH} \)
Lời giải của Tự Học 365
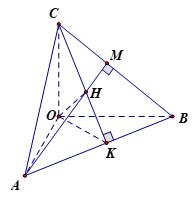
Gọi \(CK,\,\,AM\) là hai đường cao của tam giác \(ABC\).
Suy ra \(H = AM \cap CK\).
Ta có: $\left. \begin{array}{l}AB \bot \left( {OKC} \right) \Rightarrow AB \bot OH\\BC \bot \left( {AOM} \right) \Rightarrow BC \bot OH\end{array} \right\} \Rightarrow OH \bot \left( {ABC} \right)$
Mặt phẳng $\left( {ABC} \right)$đi qua điểm $H$ và nhận \(\overrightarrow {OH} \) làm một \(VTPT\)
Nên mặt phẳng $\left( {ABC} \right)$ có phương trình: \(3x - 4y + 2z - 29 = 0\).
Đáp án cần chọn là: d
Toán Lớp 12
