Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông tại \(A\), \(AB = 2a\sqrt 3 \). Đường chéo \(BC'\) tạo với mặt phẳng \(\left( {AA'C'C} \right)\) một góc bằng \(60^\circ \). Gọi \(\left( S \right)\) là mặt cầu ngoại tiếp hình lăng trụ đã cho. Bán kính của mặt cầu \(\left( S \right)\) bằng
Phương pháp giải
- Tìm tâm mặt cầu ngoại tiếp lăng trụ (cách đều các đỉnh của lăng trụ)
- Tính bán kính và kết luận đáp án.
Lời giải của Tự Học 365
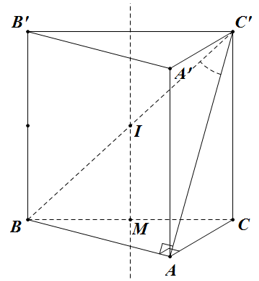
Gọi \(M\) là trung điểm \(BC\), \(I\) là trung điểm \(BC'\). Khi đó, \(IM\) là trục của đường tròn ngoại tiếp tam giác \(ABC\). Mặt khác, \(IB = IC = IB' = IC' = IA'\). Do đó, \(I\) là tâm mặt cầu ngoại tiếp lăng trụ \(ABC.A'B'C'\). Bán kính \(R = \dfrac{1}{2} \cdot BC' = \dfrac{1}{2} \cdot \dfrac{{AB}}{{\sin 60^\circ }} = \dfrac{{4a}}{2} = 2a\).
Đáp án cần chọn là: d
Toán Lớp 12
