Câu hỏi
Vận dụng
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(AD = 2a\) và \(AA' = 2a\). Tính bán kính \(R\) của mặt cầu ngoại tiếp tứ diện \(ABB'C'\).
Đáp án đúng: c
Phương pháp giải
Mặt cầu ngoại tiếp tứ diện \(ABB'C'\) cũng là mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\)
Lời giải của Tự Học 365
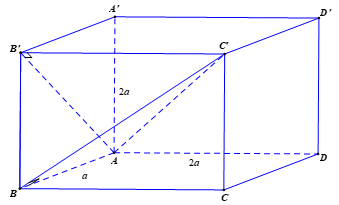
Mặt cầu ngoại tiếp tứ diện \(ABB'C'\) cũng là mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\)
Do đó bán kính là \(R = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = \dfrac{{3a}}{2}\).
Đáp án cần chọn là: c
Toán Lớp 12
