Cho một khối trụ có chiều cao bằng \(8cm\), bán kính đường tròn đáy bằng \(6cm\). Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục \(4cm\). Diện tích của thiết diện được tạo thành là :
Phương pháp giải
- Xác định khoảng cách từ trục hình trụ đến thiết diện (khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng)
- Nhận xét hình dạng của thiết diện và tính diện tích dựa vào các kiến thức đã học ở lớp dưới.
Lời giải của Tự Học 365
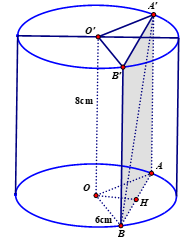
Ta có mặt phẳng \(\left( {A'AB} \right)//O'O\)
Kẻ \(A'B'//AB\) \( \Rightarrow \) thiết diện tạo thành là hình chữ nhật \(ABB'A'\)
Kẻ \(OH \bot AB,OH \bot A'A\) \( \Rightarrow OH \bot \left( {A'AB} \right)\)
\( \Rightarrow \) \(d\left( {O'O,\left( {A'AB} \right)} \right) = d\left( {O,\left( {A'ABB'} \right)} \right) \) \(= OH = 4\)
Mà \(AH = \sqrt {O{A^2} - O{H^2}} = 2\sqrt 5 \) \(\Rightarrow AB = 4\sqrt 5 \Rightarrow {S_{ABB'A'}} = 32\sqrt 5 \)
Đáp án cần chọn là: c
Toán Lớp 12
