Lời giải của Tự Học 365

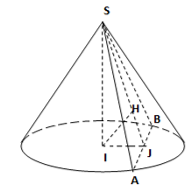
Gọi \(J\) là trung điểm của \(AB\).

Có : \(\left\{ \begin{array}{l}AB \bot IJ\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SJI} \right)\)

Nên : \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {SIJ} \right)\\\left( {SAB} \right) \cap \left( {SIJ} \right) = SJ\\IH \bot SJ\end{array} \right. \Rightarrow d\left( {I,\left( {SAB} \right)} \right) = IH = 24\)

\(\dfrac{1}{{I{H^2}}} = \dfrac{1}{{S{I^2}}} + \dfrac{1}{{{\rm{I}}{{\rm{J}}^2}}} \Leftrightarrow \dfrac{1}{{{\rm{I}}{{\rm{J}}^2}}} =  - \dfrac{1}{{{{40}^2}}} + \dfrac{1}{{{{24}^2}}} \Leftrightarrow JI = 30\)

Nên : \(BJ = \sqrt {{{50}^2} - {{30}^2}}  = 40\)

Và \(SJ = \sqrt {{{40}^2} + {{30}^2}}  = 50\)

Vậy : \({S_{\Delta SAB}} = \dfrac{1}{2}SJ.AB = \dfrac{1}{2}50.80 = 2000\left( {c{m^2}} \right).\)

Đáp án cần chọn là: d