Lời giải của Tự Học 365

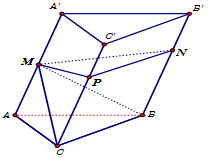
Có ${V_{A'.B'C'CB}} = \dfrac{2}{3}V = {V_{M.B'C'CB}}$

Đặt: ${V_1} = {V_{M.NPCB}} = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{NPCB}}$

$ = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).\dfrac{2}{3}{S_{CC'B'B}}$ $ = \dfrac{2}{3}.\dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{CC'B'B}} $ $= \dfrac{2}{3}{V_{M.CC'B'B}} = \dfrac{2}{3}.\dfrac{2}{3}.V = \dfrac{4}{9}V$

$\begin{array}{l}{V_2} = {V_{M.ABC}} = \dfrac{1}{3}d\left( {M,\left( {ABC} \right)} \right).{S_{ABC}}\\ = \dfrac{1}{3}.\dfrac{1}{2}d\left( {A',\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{6}V\end{array}$

Vậy \({V_{ABC.MNP}} = {V_1} + {V_2} = \dfrac{4}{9}V + \dfrac{1}{6}V = \dfrac{{11}}{{18}}V\)

Đáp án cần chọn là: d