Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).
Phương pháp giải
- Dựng góc \(\alpha \) bằng cách tìm một đường thẳng song song với \(BC\) mà góc giữa đường thẳng ấy và \(MN\) là dễ nhận thấy.
- Tính góc \(\alpha \) bằng cách sử dụng định lý hàm số \(\cos \)
Lời giải của Tự Học 365
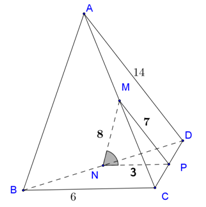
Gọi \(P\) là trung điểm của cạnh \(CD\), ta có \(\alpha = \widehat {\left( {MN,BC} \right)} = \widehat {\left( {MN,NP} \right)}\).
Trong tam giác \(MNP\), ta có \(\cos \widehat {MNP} = \dfrac{{M{N^2} + P{N^2} - M{P^2}}}{{2MN.NP}} = \dfrac{1}{2}\). Suy ra \(\widehat {MNP} = 60^\circ \).
Suy ra \(\sin \alpha = \dfrac{{\sqrt 3 }}{2}\).
Đáp án cần chọn là: b
Toán Lớp 12
