Lời giải của Tự Học 365

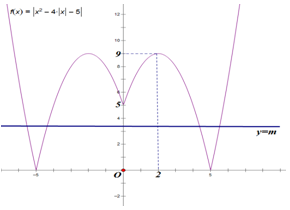
Ta có: \(\left| {{x^2} - 4\left| x \right| - 5} \right| - \dfrac{{117}}{3} = 0 \Leftrightarrow \left| {{x^2} - 4\left| x \right| - 5} \right| = \dfrac{{117}}{3}\)

Số nghiệm của phương trình \(\left| {{x^2} - 4\left| x \right| - 5} \right| - \dfrac{{117}}{3} = 0\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\) và đường thẳng \(y = \dfrac{{117}}{3}\)

Để vẽ đồ thị hàm số $y = \left| {{x^2} - 4\left| x \right| - 5} \right|$ ta vẽ đồ thị hàm số \(y = {x^2} - 4x - 5\), sau đó suy ra đồ thị hàm số \(y = {x^2} - 4\left| x \right| - 5\) bằng cách: bỏ đi phần đồ thị bên trái trục Oy, lấy đối xứng phần đồ thị nằm bên phải trục Oy qua Oy.

Từ đồ thị hàm số \(y = {x^2} - 4\left| x \right| - 5\) ta suy ra đồ thị hàm số $y = \left| {{x^2} - 4\left| x \right| - 5} \right|$ bằng cách lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua Ox sau đó bỏ đi phần đồ thị phía dưới trục Ox.

Dựa vào đồ thị thì đường thẳng \(y = \dfrac{{117}}{3}\)cắt đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\)  tại hai điểm phân  biệt nên phương trình đã cho có hai nghiệm phân biệt.

Đáp án cần chọn là: a