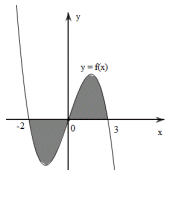
Cho đồ thị hàm số \(y = f\left( x \right)\). Diện tích S của hình phẳng (phần tô đậm trong hình dưới) là:
Phương pháp giải
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right),x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Xét dấu \(f\left( x \right) - g\left( x \right)\) trên từng khoảng xác định và phá dấu trị tuyệt đối.
Lời giải của Tự Học 365
Ta thấy diện tích hình phẳng (phần tô đậm) được giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = 0,x = - 2,x = 3\), do đó \(S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx} \) .
Dựa vào đồ thị hàm số ta thấy:
\(\begin{array}{l}f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;3} \right) \Rightarrow \left| {f\left( x \right)} \right| = f\left( x \right)\,\,\forall x \in \left( {0;3} \right)\\f\left( x \right) < 0 \Leftrightarrow x \in \left( { - 2;0} \right) \Rightarrow \left| {f\left( x \right)} \right| = - f\left( x \right)\,\,\forall x \in \left( { - 2;0} \right)\\ \Rightarrow S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} = - \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \end{array}\)
Đáp án cần chọn là: c
Toán Lớp 12
