Lời giải của Tự Học 365

Đặt \(t = \cos 3x{\rm{ }}\left( { - 1 \le t \le 1} \right)\).

Phương trình trở thành \(2{t^2} + \left( {3 - 2m} \right)t + m - 2 = 0.\)

Ta có \(\Delta  = {\left( {2m - 5} \right)^2}\). Suy ra phương trình có hai nghiệm \(\left[ \begin{array}{l}{t_1} = \dfrac{1}{2}\\{t_2} = m - 2\end{array} \right..\)

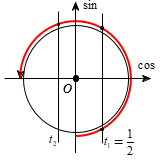
Ta thấy ứng với một nghiệm \({t_1} = \dfrac{1}{2}\) thì cho ta hai giá trị \(3x \in \left( { - \dfrac{\pi }{2};\pi } \right)\) hay có \(2\) nghiệm \(x\) thuộc khoảng \(\left( { - \dfrac{\pi }{6};\dfrac{\pi }{3}} \right).\)

Do đó yêu cầu bài toán thỏa nếu phương trình \(\cos 3x = m - 2\) chỉ có duy nhất \(1\) nghiệm thuộc \(\left( { - \dfrac{\pi }{6};\dfrac{\pi }{3}} \right)\)

Quan sát đường tròn đơn vị thì \(\left[ \begin{array}{l} - 1 < \cos 3x \le 0\\\cos 3x = 1\end{array} \right.\)  \( \Leftrightarrow \left[ \begin{array}{l} - 1 < {t_2} \le 0\\{t_2} = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l} - 1 < m - 2 \le 0\\m - 2 = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}1 < m \le 2\\m = 3\end{array} \right.\)

Đáp án cần chọn là: b