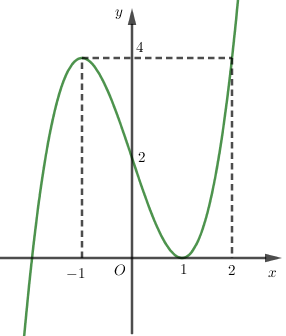
Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị bên dưới. Khi đó giá trị \(m\) để phương trình \( - {x^3} + 3x - 5m + 1 = 0\) có $3$ nghiệm phân biệt, trong đó có $2$ nghiệm âm và một nghiệm dương là
Phương pháp giải
- Biến đổi phương trình về dạng \( - 5m + 3 = {x^3} - 3x + 2\).
- Phương trình đã cho có \(3\) nghiệm phân biệt trong đó có hai nghiệm âm, một nghiệm dương \( \Leftrightarrow \) đường thẳng \(y = - 5m + 3\) cắt đồ thị hàm số đã cho tại ba điểm thỏa mãn \(2\) điểm có hoành độ âm và \(1\) điểm có hoành độ dương.
Lời giải của Tự Học 365
Ta có: \( - {x^3} + 3x - 5m + 1 = 0 \Leftrightarrow - 5m + 3 = {x^3} - 3x + 2\).
Phương trình có hai nghiệm âm một nghiệm dương \( \Leftrightarrow 2 < - 5m + 3 < 4 \Leftrightarrow - \dfrac{1}{5} < m < \dfrac{1}{5}\).
Đáp án cần chọn là: a
Toán Lớp 12
