Lời giải của Tự Học 365

Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có \(y' = \dfrac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}}\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 3\end{array} \right.\)

Bảng biến thiên:

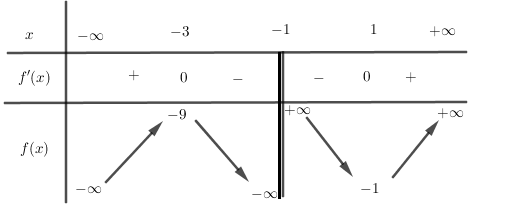
Từ bảng biến thiên ta có hàm số đạt cực đại tại điểm \(x =  - 3\), giá trị cực đại là \({y_{CD}} =  - 9\)

Đáp án cần chọn là: a