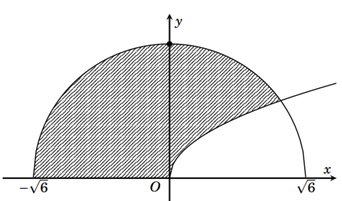
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y = \sqrt {6 - {x^2}} \) \(\left( -\,\sqrt{6}\le x\le \sqrt{6} \right)\) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay sinh bởi khi quay hình phẳng \(D\) quanh trục \(Ox\).
Phương pháp giải
Chia nhỏ miền để tính thể tích của khối tròn xoay
Lời giải của Tự Học 365
Cung tròn khi quay quanh \(Ox\) tạo thành một khối cầu có thể tích \(V=\frac{4}{3}\pi {{\left( \sqrt{6} \right)}^{3}}=8\pi \sqrt{6}\).
Thể tích nửa khối cầu là \({{V}_{1}}=4\pi \sqrt{6}\). Xét phương trình:
\(\sqrt x = \sqrt {6 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
{x^2} + x - 6 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
\left[ \begin{array}{l}
x = 2\\
x = - 3
\end{array} \right.
\end{array} \right. \Leftrightarrow x = 2.\)
Thể tích khối tròn xoay có được khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị các hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y=\sqrt{6-{{x}^{2}}}\), và hai đường thẳng \(x=0,\,\,x=2\) quanh \(Ox\) là:
\({{V}_{2}}=\pi \int\limits_{0}^{2}{\left( 6-{{x}^{2}}-x \right)\text{d}x}=\left. \pi \left( 6x-\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2} \right) \right|_{0}^{2}=\frac{22\pi }{3}.\)
Vậy thể tích vật thể tròn xoay cần tìm là \(V={{V}_{1}}+{{V}_{2}}=4\pi \sqrt{6}+\frac{22\pi }{3}\).
Đáp án cần chọn là: d
Toán Lớp 12
