Trong mặt phẳng tọa độ Oxy, gọi \(\left( {{H_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2}}}{4};\,\,y = - \frac{{{x^2}}}{4};\,\,x = - 4;\,\,x = 4\) và \(\left( {{H_2}} \right)\) là hình gồm tất cả các điểm \(\left( {x;y} \right)\) thỏa \({x^2} + {y^2} \le 16;\,\,{x^2} + {\left( {y - 2} \right)^2} \ge 4;\,\,{x^2} + {\left( {y + 2} \right)^2} \ge 4\)
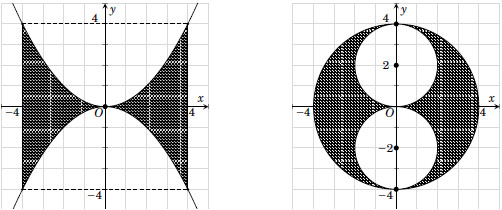
Cho \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\) quanh quanh trục Oy ta được các vật thể có thể tích là \({V_1},\,\,{V_2}\). Đẳng thức nào sau đây đúng ?
Phương pháp giải
Sử dụng các công thức tính thể tính khối trụ, khối cầu và ứng dụng tích phân để tính thể tích của vật thể tròn xoay.
Lời giải của Tự Học 365
\({V_1}\) là hiệu thể tích khối trụ có bán kính đáy bằng $4$, chiều cao bằng $8$ với hai lần thể tích của vật thể tròn xoay tạo thành khi vật thể bị giới hạn bởi các đường \(x = 2\sqrt y ;\,\,x = 0;\,\,y = 0;\,\,x = 4\) quay quanh trục $Oy$.
\( \Rightarrow {V_1} = \pi {.4^2}.8 - 2\pi \int\limits_0^4 {4ydy} = 64\pi \)
\({V_2}\) là hiệu thể tích khối cầu có bán kính bằng $4$ với $2$ lần thể tích khối cầu có bán kính bằng $2$.
\( \Rightarrow {V_2} = \dfrac{4}{3}\pi \left( {{4^3} - {{2.2}^3}} \right) = 64\pi \)
Vậy \({V_1} = {V_2}\).
Đáp án cần chọn là: b
Toán Lớp 12
